Maestro Bogomolny’s last Quiz

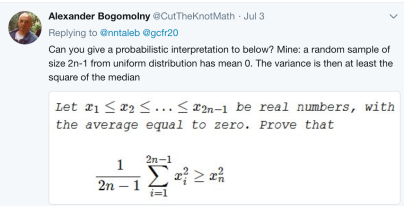
Screen Shot 2018-08-13 at 8.18.05 AM.png

Background: Maestro Bogomolny was interested in a probabilistic interpretation of the above, having noticed an earlier derivation that relied on the behavior of Poisson sums under the law of large numbers. For in a forcoming paper, the following was derived “probabilistically”:

$e^{-n}\sum _{m=0}^{n-1} \frac{n^m}{m!}= \frac{1}{2} +O\left(\frac{1}{\sqrt{n}}\right)$
From the behavior of the sum of Poisson variables as they converge to a Gaussian by the central limit theorem: $e^{-n} \sum _{m=0}^{n-1} \frac{n^m}{m!} = \mathbb{P}(X_n < n)$ where $X_n$ is a Poisson random variable with parameter $n$ . Since the sum of $n$ independent Poisson random variables with parameter $1$ is Poisson with parameter $n$ , the Central Limit Theorem says the probability distribution of $Z_n = (X_n - n)/\sqrt{n}$ approaches a standard normal distribution. Thus $\mathbb{P}(X_n < n) = \mathbb{P}(Z_n < 0) \to 1/2$ as $n \to \infty$ .